Operaciones en Q/R( suma, resta, división y multiplicación)

Aquí vamos a discutir las operaciones de números racionales como la suma, resta, multiplicación, división, potenciación y sacar su factor común:

Suma de números racionales

Para sumar y restar números racionales existen dos casos diferentes con los cuales podemos tratar, el primero es cuando poseen un denominador distinto entre los sumandos, y el otro es cuando tienen un denominador de igual valor y es por este por el que vamos a empezar.

Cuando resolvemos la adición de números racionales y la sustracción de números racionales con igual denominador, simplemente se mantiene el mismo denominador (que es el valor ubicado en la parte inferior de la fracción) y sumamos o restamos los numeradores (en la parte superior de la fracción) según sea el caso:

Cuando tenemos denominadores de distinto valor, lo que tenemos que hacer es buscar una fracción equivalente, y encontrar el mínimo común múltiplo de los denominadores a través de multiplicaciones o divisiones que los igualen y formen fracciones equivalente, tomando en cuenta que cualquier operación realizada debe también realizarse al numerador para no alterar el resultado, veamos:

Multiplicación de números racionales

La multiplicación entre fracciones es sencilla si se sabe cómo hacer. En primer lugar, se multiplican los numeradores de todos los factores y a continuación el producto resultante se lo utiliza como numerador, luego se multiplican los denominadores y al resultado se lo ubica como denominador sin importar si el valor es igual o distinto, de esta manera:

División de números racionales

Para dividir los números racionales, tomamos el numerador de la primera fracción y se lo multiplica por el denominador de la segunda fracción y este resultado será utilizado como numerador; a continuación se toma el denominador de la primera fracción y se lo multiplica por el numerador de la segunda fracción, y a ese resultado se lo ubica como denominador. Por lo tanto en el caso de la división, el orden de los cocientes si altera el resultado, veamos el siguiente ejemplo:

Como se puede notar, para dividir los números racionales, se debe multiplicar en cruz, tomando en cuenta que el numerador y el denominador de la primera fracción no cambia de orden, pero los de la segunda fracción si lo hacen para lograr el resultado final.

Potenciación de números racionales

Para la potenciación de un número racional, se deben seguir estas simples reglas:
Si el número racional posee distintas potencias para distinto numerador y el denominador, solo se procede a potenciar cada cociente y simplificar si es posible:

Potencias con exponente cero

La potencia con exponente cero es igual a 1.

Potencia de producto de fracciones

La potencia de un producto de fracciones es igual al producto de las potencias de los factores.

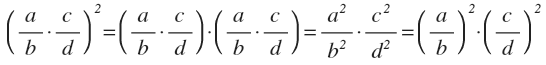
Potencia de cociente de fracciones

La potencia de un cociente de fracciones es igual a al potencia del dividendo entre la potencia del divisor.

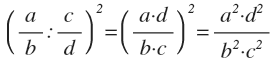
Multiplicación de potencias de la misma base

Para multiplicar dos potencias de la misma base, se suman los exponentes.

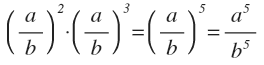
Cociente de potencias de la misma base

Para dividir dos potencias de la misma base, se restan los exponentes.

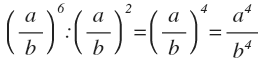
Potencia de otra potencia

Para calcular la potencia de otra potencia se multiplican los exponentes.